Alors ma première idée était de présenter de façon théorique les mathématiques sous jacente au machine learning et au deep learning cependant, bien que les quelques outils essentiels se résument globalement à la manipulation de vecteur, de l’utilisation du calcul matriciel, des combinaisons linéaires, d’algo d’apprentissage, des dérivées partielles (de fonction de coûts, d’erreurs quadratiques) et quelques notions en probabilités, cela fait énormément de base théorique à développer.
Or même si l’envie y est, je n’ai pas forcément le temps de développer tout cela. En fait il faudrait globalement replonger dans la moitié du programme de math de classe prépa, et si d’une part, la masse est conséquente, je ne pense pas que cela soit franchement pertinent pour aborder ensuite ce qui nous intéresse vraiment : l’IA.
Deja que globalement, en employant les frameworks adéquats du domaine, aujourd’hui, une bonne partie même des aspects mathématiques peuvent être masqués. Et si l’on a une bonne connaissance du comportement que l’on peut attendre de tel ou tel algo ou fonction de coût, il est presque inutile d’aborder ces sujets. Cependant, ceci est une vision très réductrice et je pense qu’une connaissance même succincte de la forme de ces algorithmes et que savoir quels sont les mécanismes de calcul sous jacent est un plus pour parfaire et optimiser nos choix sur le traitement des données et le choix des modèles à employer.
Partie Espace vectoriel
Bien nous allons aborder les bases supportant le domaine du machine learning. en l'occurrence ici les espaces vectoriels. Ne partez pas en courant, c’est juste pour dire que l’on a utiliser des vecteurs et des matrices!Pour aborder le sujet, nous considérerons dans la suite de l'article deux espaces vectoriels
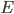 et
et 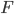
de base respectivement
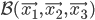 et
et 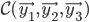
Les vecteurs
Ainsi on appellera vecteur tout triplet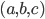 noté
noté 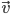
définie dans
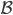 tel que
tel que 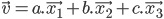
ou de façon généralisée:
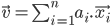
Par convention on pourra noter le vecteur comme suit (notation vectorielle) :
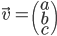
La définition du vecteur que nous avons utilisé précédemment par la combinaison linéaire des éléments de
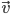 avec les vecteurs de base va nous permettre plein de chose.
avec les vecteurs de base va nous permettre plein de chose. La multiplication par un scalaire tel que:
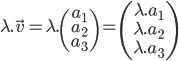
L’addition de deux vecteurs:
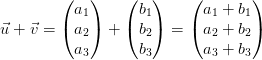
On peut évidement évoquer le produit scalaire ou le produit vectoriel (souvent vu en géométrie euclidienne et utile en mécanique) mais ceux ci ne nous apporteront pas immédiatement grand chose a part dans les Machines a vecteurs de support (SVM)[1] mais nous y reviendrons.
Pour introduire le produit scalaire, il nous faut d'abord la notion de projection. Ainsi la projection d'un vecteur sur un autre, permet de construire un nouveau vecteur dirigé par
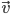 normalisé [2] tel que:
normalisé [2] tel que: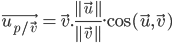
Ainsi si l'on considère le produit scalaire
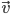 ,
, 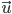 défini dans la même base
défini dans la même base 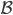 alors on a un valeur scalaire telle que:
alors on a un valeur scalaire telle que: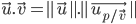
ou plus habituellement
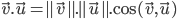
A noter que dans le cas ou les deux vecteurs sont définis dans des base differentes, il sera nécessaire d'appliquer une transformation a l'un des deux vecteur afin que celui ci soit définit dans la même base.
Pour cela, il est nécessaire de définir les combinaisons linéaires de passage de la première base vers la seconde (faire la réciproque permettra d'obtenir le résultat dans la base initiale). Pour cela, nous verrons que l'utilisation des matrices, bien que pas forcement nécessaire, sera d'une grande aide.
Maintenant si l'on considère le produit vectoriel
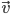 ,
, 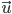 défini dans la même base
défini dans la même base 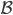 alors on obtient un nouveau vecteur
alors on obtient un nouveau vecteur 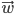 tel que:
tel que: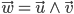
avec les propriétés suivantes:
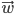 est orthogonal a
est orthogonal a 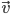 et
et 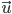 . (leur produit scalaire est nul) formant une base direct.
. (leur produit scalaire est nul) formant une base direct.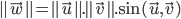
Les matrices
Considérons toujours les deux espaces vectoriels précédemment donnés munis de leur base respective. Considérons l'application: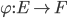
Ainsi tous les vecteurs de
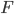 admettent une décomposition selon un ensemble de vecteurs de
admettent une décomposition selon un ensemble de vecteurs de 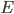 tel que les vecteurs de base on a:
tel que les vecteurs de base on a: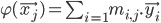
On notera alors M l'ensemble des paramétres m organisés selon une grille a i ligne et j colonne:
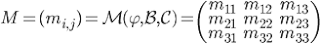
Ainsi on a pour tous les vecteurs
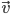 et
et 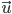 de
de 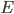 et
et 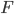 , les matrices colonne V et U telle que:
, les matrices colonne V et U telle que: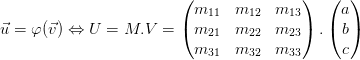
Nous ramenant au système d’équations:
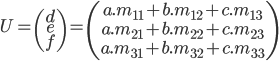
Ceci définissant les bases sur la nature des matrices, je vous invite a vous projeter dans quelques documents plutôt simple a comprendre afin d'en percevoir le très grand potentiel de cet outil [3].
On peut donc maintenant passer aux opérations de base sur les matrices que sont les additions et la multiplication (attention celle ci n'est pas commutative). Considérons alors pour la suite les matrices 3X3, A et B .
L'addition matricielle:
Maintenant que nous avons traités des structures nécessaires au machine learning, intéressons nous aux algorithmes. Globalement, nous avons vu ce que nous allions manipuler pour l'IA mais il reste encore les traitements particuliers qui peuvent être utiliser.
Par exemple, il nous faudra être capable d’évaluer l'erreur que fait notre modèle de machine learning en utilisant par exemple l'erreur quadratique moyenne ou (MSE, mean square error). Celle-ci étant utilisé très souvent sous differentes formes et déclinaison afin d'une part mesurer la performance des modèles et procéder a leur apprentissage, il est intéressant d'en présenter quelques notions.
L'erreur quadratique moyenne permet la mesure globale de l’écart entre la valeur désirée et celle obtenue calculé sous la forme d'une moyenne. Celle ci est construite de façon quadratique pour que les erreurs ne se compensent pas autour de la moyenne.
L'erreur moyenne se définit tel que:
L'erreur quadratique moyenne se définit tel que:
A noter que généralement on utilise l'erreur quadratique sans la racine puisque utiliser de façon continue sur l'ensemble des données, la mesure de performance reste homogène. La notation chapeau représente la valeur estimé par le modèle (donc la fonction dépendante des paramètres du modèle qui sont à ajuster), en opposition avec celle réelle.
Sur la base de l'erreur quadratique pourront etre ajouté divers paramètres complémentaires permettant un ajustement dynamique des paramètres du modèle. L'apprentissage sera alors plus ou moins efficace et ou rapide, sachant que généralement, ces deux propriétés seront assez antagoniste.
Enfin de façon a permettre un apprentissage efficace, on procédera au calcul du gradient de l'erreur (c'est a dire l'ensemble des dérivés de la fonction selon l'ensemble de ses paramètres). Celle ci aura l’intérêt de garantir la convergence de la procédure d'apprentissage en garantissant l'orientation de la correction a appliquer au fils des itérations d'apprentissage.
Sans entrer dans le détail, si l'on considére la fonction suivant:
Voila, je ne pense pas que cette liste est exhaustive des outils mathématiques nécessaires a l'IA mais pour tous ceux manquant (comme les fonctions d'activations possible), nous prendrons le temps de les explicités le moment venu au cas par cas. En tout cas nous voyons rapidement que le domaine de l'IA nécessite de bonnes et larges bases théoriques comme technique (nous le verrons dans les prochains articles).
Références:
[1] https://zestedesavoir.com/tutoriels/1760/un-peu-de-machine-learning-avec-les-svm/[2] https://fr.wikipedia.org/wiki/Norme_(math%C3%A9matiques)
[3] https://webusers.imj-prg.fr/~nicolas.laillet/Methodo1.pdf


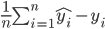
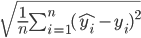



Aucun commentaire:
Enregistrer un commentaire