Les automates à états sont, par définition, des outils
mathématiques permettant la modélisation et la manipulation de langages
décrivant le comportement des SED. Ils peuvent avoir une représentation
graphique grâce aux diagrammes à états permettant une analyse visuelle.
Un
automate à état, est un n-uplet noté G=(X, S, f, x0,
Xm) tel que :
·
X : Ensemble des états
de l’automate.
·
S : Alphabet ou ensemble
des événements réalisables par l’automate.
·
f : Relation de
transition qui définit pour un état courant et un événement appartenant à
l’alphabet un second état qui devient l’état courant.
·
x0 : l’état initial de
l’automate
·
Xm : l’ensemble des
états marqués de l’automate permettant la validation de séquence d’événements.
Exemple:Si G un automate tel que :
X = {0,1,2}
S = {a,b,c}
f = {(0,a)->1,(1,b)->0,(1,c)->1,(0,c)->2}
x0= 0
Xm= {1}

Ce type d’automate est très général et peut avoir un nombre infini d’états empêchant une implémentation concrète. Dans cette étude on se limite aux automates à états finis qui se caractérisent par le fait que l'ensemble des états doit être fini. Les automates à états finis sont des implantations pour les langages dits réguliers
Langage des automates à états finis
Un automate à états finis décrit deux langages, comme illustré par la figure 8. Le premier langage est dit le langage généré par l’automate. Il correspond à toutes les possibilités de transitions offertes par la relation de transition. Le second langage est le langage marqué, il correspond à la réalisation de toutes les possibilités de transitions offertes par la relation de transition menant à un état final marqué. Le marquage est utile dans le cadre de la définition de comportements valides pour l’automate.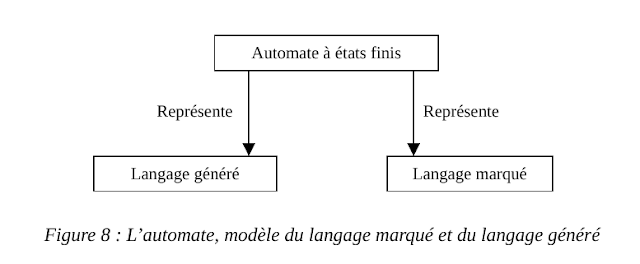
L’utilisation d'un automate à états finis permet de voir un SED dans sa globalité grâce au langage généré mais aussi de voir ce SED dans son comportement souhaité via le langage marqué. La différence entre ces deux langages permet de définir le langage bloquant de l’automate. En effet, le langage marqué est inclus ou égal au langage généré de l’automate. La caractérisation du langage bloquant d’un automate est alors mise en évidence par la différence des langages marqués et générés comme cela est illustré par la figure 9. Mathématiquement, pour un automate G, avec L(G) son langage généré et Lm(G) son langage marqué, l’automate est bloquant si Lmpréf(G) inclu dans L(G). Il est non bloquant si Lmpréf(G)=L(G).

Exemple:Si G un automate, illustré en figurer 10, tel que:
X = {0,1,2}
= {a,b,c}
f = {(0,a)->1,(1,b)->1,(0,c)->2}
x0 = 0
Xm = {1}On a:
L(G) = {epsilon, c, ab*}
Lm(G) = {ab*}
Lmpréf(G) = {epsilon, ab*}Et Lmpréf(G) inclu dans L(G) donc G est bloquant (voir figure 10)

Opérations sur les automates à états finis
Les automates d’états finis étant les modèles des langages réguliers, toutes les opérations présentées sur les langages leur sont applicables. Certaines variations existent dans les termes utilisés pour les nommer. Il est donc nécessaire de les présenter dans le détail afin de clarifier la dénomination utilisée.Calcul de la partie accessible : L'opération calculant la partie accessible d'un automate supprime les états dans l'automate à la suite d’une séquence d’évènements.
Calcul de la partie coaccessible : L'opération de permet de rendre non bloquant un automate bloquant en supprimant les états à partir desquels il n’existe pas de séquences d’évènements permettant d’atteindre un état marqué.
Opération Trim
L’opération Trim réalise successivement les opérations d'accessibilité et de coaccessibilité ou inversement. Cette opération est importante car elle permet de rendre le langage généré de l'automate égal à la fermeture préfixée du langage marqué. (L(G)=Lmpréf(G))Exemple:
Dans l’automate G, illustrée par la figure 11, l'état 3 n'est pas accessible et l'état 2 ne permet pas d'accéder à un état marqué. Via l'opération Trim, ces états seront supprimés (figure 12)

Projection
La projection d'un automate est directement issue de la projection des langages puisqu'un automate est le modèle d'un langage. Même si le mécanisme reste le même au niveau langage, il est un peu plus complexe à mettre en œuvre au niveau d'un automate. Pour projeter un automate, il faut identifier les transitions à supprimer et ensuite raccorder les états afin de restaurer le langage projeté.Exemple:
La projection, illustrée par les figures 13 et 14, de l’automate G de langage L(G)={bd,abc} sur l’alphabet ={b,d} renvoie un automate dont le langage est P(L,)={b,bd} conforme à la projection définie pour les langages.

Remarque:
Le résultat peut donner un automate à états finis non déterministe. En effet, sur la figure 14 de l’exemple, l’état 0 génère un événement b menant à l’état 2 et 4.
La projection peut rendre des états non atteignables.
Projection inverse
De la même façon que la projection inverse d'un langage, sur un automate cette opération va compléter chaque état avec les événements non présents dans l'alphabet de l'automate.Exemple:
La projection inverse, illustrée par les figures 15 et 16, d’un automate G de langage L(G)={ab} définit sur l’alphabet ={a,c} renvoie un automate G’ de langage L(G')={c*ac*bc*}.

Il faut noter que l’évènement "a" faisant déjà partie de l'alphabet n'a pas fait l'objet de l'opération de projection inverse. En terme de SED et d'état, cela signifie que "a" est une action importante qui ne peut être ignorée, contrairement à l’événement "c" qui sera ignoré (en terme d’évolution de l’automate, pas en terme de langage) puisqu'il reste dans l'état courant.
Union
L’union fusionne les états initiaux des différents automates réalisant ainsi l'union des langages. Cette opération peut également amener à un automate non déterministe si les états initiaux génèrent des évènements identiques, comme illustré par les figures 17, 18 et 19.Exemple:


Produit libre
Le produit libre entre automates permet la fusion de leur langage, cela signifie qu’il est toujours possible d’évoluer à chaque instant dans l’automate résultant de cette opération, de la même façon que les automates d’origines fonctionnant en parallèle. En terme de SED, cela correspond à la visualisation de deux systèmes fonctionnant en parallèle sans communication ni synchronisation. Le langage résultant de cette opération est donc bien plus important que leur simple somme qui correspondrait plutôt à l'union. Ainsi cette opération met en évidence que la modélisation des SED devient rapidement complexe dès que de nombreux systèmes mis en parallèles sont modélisés. Le produit libre est illustré en figure 20 montrant toutes les combinaisons des deux automates, il est noté ||.
Exemple:
Cet exemple illustre plus concrètement le produit libre de deux automates, G1 (figure 21) et G2 (figure 22). La figure 23 illustre la complexité du résultat des deux automates (de l’ordre n*m, n étant le nombre d’états du premier automate et m celui du second).

Produit strict
Le produit strict (ou produit cartésien dans la littérature [10], [1]) est une opération permettant de réaliser l'intersection des langages. Comme illustré par les figures 24, 25 et 26, cette opération réalise le produit cartésien des états et relie ces derniers sur les transitions communes aux différents automates.En terme de SED, le produit strict représente la synchronisation totale des systèmes. Ils doivent réaliser les mêmes actions en même temps, si cela n'est pas possible alors aucune action n'est réalisée. Le produit strict est noté x.
Exemple:

Produit synchronisé
Le produit synchronisé est un produit permettant de modéliser le comportement de plusieurs SED mis en parallèle (comme pour le produit libre). Les automates dont certains événements de leur alphabet sont synchronisés transitent ensemble sur ces derniers, les autres évènements restant libres. Plusieurs cas sont à prendre en compte. Si les alphabets sont totalement disjoints, le produit synchronisé revient à la réalisation d'un produit libre. Si les alphabets sont égaux, le produit synchronisé revient à la réalisation d'un produit strict. Si les alphabets ont une intersection non vide alors la combinaison des deux opérations (libre et strict) est réalisée puisque le comportement commun est extrait sur les évènements communs, et les comportements libres des automates sont ajoutés pour les évènements non communs.Le produit synchronisé a la particularité d’être réalisable à partir d’opérations déjà définies comme la projection inverse et le produit strict, comme illustré par les figures 27, 28 et 29. Si L1 et L2 sont deux langages alors L3=intersect(IP(L1,2),IP(L2,1)) est le produit synchronisé. Pour plus de souplesse, ce produit est noté L3=L1 ||s L2. Il est nécessaire de préciser que la manipulation des alphabets permet de modifier la configuration du produit synchrone et donc son résultat, un événement défini dans l'alphabet ne se trouve pas forcement dans la relation de transition de l'automate, comme illustré par les figures 30, 31 et 32.
Exemple:
Si L1(G1)={(ab)*} et L2(G2)={(ac)*} avec 1={a,b} et 2={a,c} alors L(G1||sG2)=intersect(IP(L1,2),IP(L2,1))={(a(bc|cb))*}

Par contre, si 1={a,b,c} et 2={a,c,b} avec L1(G1)={(ab)*} et L2(G2)={(ac)*} alors L3=interssect(IP(L1,2),IP(L2,1))={a} c’est à dire le produit strict.

Remarque sur les automates d’états finis non déterministes
Le problème du déterminisme dans les automates à états apparaît dans de nombreuses opérations comme celle de projection ou d’union ou encore du produit libre. Le non-déterminisme d’un automate est caractérisé par une particularité dans la relation de transition. Cette particularité est que pour un état et un évènement donné, la relation de transition donne deux états possibles. Dans le cadre d’une implémentation et d‘une exécution, il est impossible de définir dans quel état se trouve l’automate.En terme de langage, la notion de déterminisme n’existe pas [1] et [10], par contre la théorie des langages définis que s’il existe plusieurs automates modèles d’un même langage, ces derniers peuvent être déterministes ou non. Il existe une relation d’équivalence (en terme de langage) entre ces automates permettant de transformer un automate non déterministe en un automate déterministe tout en préservant le langage comme illustré par les figures 33 et 34. Il est nécessaire de noter qu’un automate possédant plusieurs états initiaux est considéré comme non déterministe car il est possible de construire un état initial à partir duquel partiront des transitions epsilons allant vers chaque état initial de l’automate.
Exemple :

Conclusions
La théorie des langages et des automates à états offre un cadre idéal à la modélisation et à la manipulation des SED grâce aux diverses opérations comme le produit synchronisé ou celles issues de la théorie des ensembles comme l’union, le produit strict etc. De nombreuses particularités sont aussi à prendre en compte afin de rester dans un cadre d’implémentation réalisable comme les problèmes liés au non-déterminisme ou la nécessité d’utiliser les langages réguliers et les automates à états finis. Les éléments présenté dans ce chapitre sont les bases essentielles à l’étude de la théorie de la supervision définie par P.J.Ramadge et W.M.Wonham.References
[1] Ramadge P.J., Wonham W.M. The control of discrete-event systems. IEEE Transactions on Automatic Control, 1989, Vol. 77, N° 1, p. 81-98.[10] C. G. Cassandras, and S. Lafortune. Introduction to discrete event systems, Kluwer Academic Publishers, 1999, ISBN: 0-7923-8609-4
Aucun commentaire:
Enregistrer un commentaire