Thématiques principales

lundi 24 septembre 2018

Python : Manipulation des données

Nous voila dans une petite digression. Je n'avais pas pensé faire un article sur les préceptes de base de la manipulation des listes, des tuples, des tableaux ou encore des dictionnaires en python mais au vue des quelques derniers articles sur l'IA [1-4] et aussi des futurs articles qui auront pour base les frameworks numpy [6], pandas [7] et scikit-learn [8], il nous faut explorer un peu comment nous pouvons manipuler les données, c'est a dire ici les charger, et effectuer des calculs.

Alors nous irons dans la compréhension des structures de données rencontrées de façon récurrente dans l'IA et le machine learning mais nous n'entrerons pas ici dans la visualisation ou l’interprétation des données. Nous nous attarderons sur ces aspects lorsque l'on traitera de la visualisation et de l'analyse statistique des données dans la limite du compréhensible.

Commençons par les bases, ce que python nous permet de base déjà

Les listes

Bon nous ne cherchons pas spécialement a faire un cours sur python donc voyons l'essentielle sur les listes et les manipulations de base. La liste en python est un ensemble de données de taille dynamique et modifiable.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
# liste
maListe=[1, 2, 3, 4]
print(maListe)
maListe.append(5)
print(maListe)
print(maListe[:3])#on prend les paramtres avant l'index 3 exclu
print(maListe[3:])# on prend les paramtres apres l'index 3 inclu
malisteN2=[[1, 2, 3, 4],[5,6,7,8],[9,10, 11, 12],[13, 14, 15, 16]]
print(malisteN2)

[1, 2, 3, 4]
[1, 2, 3, 4, 5]
[1, 2, 3]
[4, 5]
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]


Pour les manipulation usuelles propres a l'informatique, on retrouvera les méthodes habituelles telles que del, insert, remove, etc... et bien sur les while ou les for.


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#Manip des liste
for elt in maListe:
    print(elt)
    
for i,elt in enumerate(maListe): # c'est parceque ca nous renvoie un tuple
    print(i,elt)
    
maCompreh=[i*elt for i,elt in enumerate(maListe)]
print(maCompreh)
maCompreh=[i*elt for i,elt in enumerate(maListe) if  elt<4]
print(maCompreh)


1
2
3
4
5
0 1
1 2
2 3
3 4
4 5
[0, 2, 6, 12, 20]
[0, 2, 6]

Les tuples

Les tuples a l'image des listes sont des ensembles de données mais non modifiable (on dit immutable)
Les tuples sont pratiques pour lier des données entre elles. Si l'on considère les données personnelles d’individus sous la forme d'un tableau, alors généralement, les colonnes seront modélisé via des listes alors que les lignes (en gros des données d'un individu en particulier) seront plus naturellement construit sous la forme de tuple.


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
a,b=12,13
print(a)
print(b)
tuple=(a,b)
print(tuple)
print(a,b)

listeDeTuple=[(1,1),(2,2),(3,3)]
print(listeDeTuple)

for (a,b) in listeDeTuple:
    print(a+b)

12
13
(12, 13)
12 13
[(1, 1), (2, 2), (3, 3)]
2
4
6

A noter que l'utilisation des tuples est une façon elegante de gérer un passage de paramètre de fonction dont on ne connait pas le nombre d'argument. De même il est possible de réaliser le même genre d'approche avec les dictionnaires.

Les dictionnaires

Les dictionnaires sont encore un autre type de structure de données. Un dictionnaire fonctionne sur le principe du stockage clef, valeur. La clef est unique et référence une donnée qui est accessible par la clef.

Quelques exemple parlerons plus simplement.


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#les dictionnaires
monDico={"toto":12,"tata":14}
monDico["titi"]=45
print(monDico)
print(monDico.pop("toto"))
print(monDico)

for key in monDico: #equivalent a monDico.keys()
    print(key)

for value in monDico.values():
    print(value)    
    
for key,value in monDico.items():
    print(key,value)

{'toto': 12, 'tata': 14, 'titi': 45}
12
{'tata': 14, 'titi': 45}
tata
titi
14
45
tata 14
titi 45

Les fonctions

Petite digression sur les fonctions: comme tout langage de programmation, python utilise le concept de fonction (ca serait bien dommage au passage). Au delà de l'utilisation des structure de données classique et de leur API, il est souvent nécessaire de construire nos propres algorithme afin de construire et transformer l'information (c'est d’ailleurs un peu le propre de l'informatique....) Donc ce point au delà d'une petite digression est relativement important car il permet d'aller au delà de ce que vont nous fournir les frameworks.


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
#Definition d'une fonction
def uneFuntion():
    print("C'est ma fonction")

#utilisation dans list et dictionnaire    
fdic={'theFunc':uneFuntion}
fdic['theFunc']()

flist=[uneFuntion]
for f in flist:
    f()   

#passage de paramtres specifique en utilisant des fonctions
def uneAutre(*params,**dic):
    for f in params:
        f()
    dic["theFunc"]()

#resultat
uneAutre(uneFuntion,theFunc=uneFuntion)

Les fonctions sont un indispensable. Ici je n'irais pas plus loin comme avec les lambda ou les classes qui sont dans le cadre de l'IA, surtout un moyen d'industrialiser, chose que nous verrons probablement mais plus tard car il reste du chemin a parcourir avant.

A noter cependant que pour certaines choses comme les boucles, la consommation en temps de calcul peut être conséquente surtout dans l'IA et le BigData, Heureusement, les frameworks que nous allons voir dans le suite de cet article apportent certaines optimisation permettant de palier a ce problème. Ainsi, avant de s'aventurer a réinventer la roue, assurez vous qu'une solution efficace n'y a pas déjà été proposée (dans le doute faites des comparaisons avec la commande Juyter %timeit ).

Les frameworks

Nous entrons maintenant la partie permettant la manipulation des données propres a l'IA en gros les matrices comme nous l'avions vu dans l'article sur les notions mathématiques [8].

Pour commencer on va s’intéresser a Pandas, ensuite Numpy/Scipy et enfin les jeux de données de scikit-learn. Pour ce qui est de la visualisation de données, on traitera cela dans un article spécifique.

Numpy

On va commencer par Numpy, ce framework étant le plus accessible pour acquérir les bases. En effet, sans entrer dans le détail de toutes les fonctionnalités de NumPy, ce framework va nous permettre de faire les manipulations usuelles sur les vecteurs et les matrices.

Entre autres, a partir des listes que nous avons utilisées précédemment, il va nous être possible de construire facilement des vecteurs ou des matrices grâce à la fonction array.


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
import numpy as np

arr=np.array(maListe)
print(arr)
print(arr.T)
arr2=np.array(malisteN2)
print(arr2)
print(arr2.T)
print(arr[:3])# le slicing marche sur les array
print(arr2[0])
print(arr2[1][3])# aller chercher l'oject a l'index 1,3
print(arr2[:2])# on recuper 2 ligne
print(arr2.T[:2].T) #quand on veut recuperer deux colones, pas le choix, on transpose avant et apres.... 
#voir s'il n'y a pas de solutiion plus sympas


Dans cette exemple, on peut voir que la méthode array s'appuie sur la dimension de la liste afin de déterminer si elle doit produire un vecteur ou une matrice. Dans le cas ou il est nécessaire de construire forcement une matrice même en ayant un liste de dimension 1, il faudra changer de méthode et utiliser mat.


1
2
3
4
5
6
mat1=np.mat(maListe)
print(mat1)
print(mat1.T)
mat2=np.mat(malisteN2)
print(mat2)
print(mat2.T)


Ceci part du principe que l'on dispose d'une liste déjà construire cependant ce n'est pas toujours le cas. Numpy permet alors de construire des vecteurs par extension grâce à la méthode arange (avec un paramétrage spécifique de cette fonction, il sera aisé de construire une suite de données avec un échantillonnage particulier, pour aller plus loin, il faudra utiliser linspace. Pour les matrices on s’appuiera sur la méthode reshape. (A noter que Numpy intègre aussi un générateur de nombre aléatoire permettant de construire des matrices de données aléatoires mais aussi des outils de calcul de moyenne, de variance, l'ecart typeetc...)


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
listeParExtension=np.arange(16)# nombre d'element a produire
print(listeParExtension)
arrayExt=listeParExtension.reshape(4,4)
print(arrayExt)

listeEchantil=np.arange(4,13,0.1)# depart, fin(exclu), pas d'echantillionnage 
print(listeEchantil)
np.linspace(1., 4., 25)# debut, fin, nbr elements a produire uniformement reparti

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15]
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]
[ 4.   4.1  4.2  4.3  4.4  4.5  4.6  4.7  4.8  4.9  5.   5.1  5.2  5.3
  5.4  5.5  5.6  5.7  5.8  5.9  6.   6.1  6.2  6.3  6.4  6.5  6.6  6.7
  6.8  6.9  7.   7.1  7.2  7.3  7.4  7.5  7.6  7.7  7.8  7.9  8.   8.1
  8.2  8.3  8.4  8.5  8.6  8.7  8.8  8.9  9.   9.1  9.2  9.3  9.4  9.5
  9.6  9.7  9.8  9.9 10.  10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 10.9
 11.  11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 12.  12.1 12.2 12.3
 12.4 12.5 12.6 12.7 12.8 12.9]


Pour construire des matrices justement, il est parfois nécessaire de construire des matrices spécifiques comme l'identité ou unitaire. Pour cela, on utilisera les fonctions ones et eye que l'on combinera avec quelques opérations ou la méthode concatenate.


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
print(np.eye(2,2))
print(np.ones((1,2)))
print(np.concatenate((np.eye(2,2),np.ones((1,2))),axis=0))
print(np.concatenate((np.eye(2,2),np.ones((2,1))),axis=1))# la transposé de la precedente

[[1. 0.]
 [0. 1.]]
[[1. 1.]]
[[1. 0. 1.]
 [0. 1. 1.]]
[[1. 0. 1.]
 [0. 1. 1.]]


Enfin, pour obtenir des matrices diagonales avec des paramètres spécifiques sur la diagonales, on utilisera la fonction diag (Cela nous facilitera la vie quand on sera amener a calculer et utiliser le spectre de notre espace vectoriel)


1
2
3
4
5
6
7
8
9
forDiag=np.arange(6)
np.diag(forDiag) # va savoir a quoi ca peut bien servir?

array([[0, 0, 0, 0, 0, 0],
       [0, 1, 0, 0, 0, 0],
       [0, 0, 2, 0, 0, 0],
       [0, 0, 0, 3, 0, 0],
       [0, 0, 0, 0, 4, 0],
       [0, 0, 0, 0, 0, 5]])

On parlait de faire des opérations, au delà de réaliser des opérations standard sur les matrices, on pourra spécifier le sens de ces opérations grâce au paramètre axis


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
liste9=np.arange(9)
mat33=liste9.reshape(3,3)
print(mat33+mat33)
print(mat33*mat33)
matM=np.dot(mat33,mat33)
print(matM)
print(matM[matM<50])
print(mat33)
print(np.sum(mat33))
print(np.sum(mat33,axis=0))# sommes des lignes
print(np.sum(mat33,axis=1))# sommes des colonnes

[[ 0  2  4]
 [ 6  8 10]
 [12 14 16]]
[[ 0  1  4]
 [ 9 16 25]
 [36 49 64]]
[[ 15  18  21]
 [ 42  54  66]
 [ 69  90 111]]
[15 18 21 42]
[[0 1 2]
 [3 4 5]
 [6 7 8]]
36
[ 9 12 15]
[ 3 12 21]

Dans Numpy il reste encore de très très nombreuses fonctionnalités mais cet article ne suffira pas pour toutes les présenter. Avec ces quelques exemples pourtant, nous avons déjà une bonne partie des manipulation de base que nous voudrions faire entre autre sur les matrices.

Pandas

Le framework suivant que nous allons présenter est Pandas. Pandas est un outils d'analyse de données, c'est a dire que si Numpy est un outils vraiment dédié au calcul, Pandas s’intéressera plutôt a la sémantique de données et leur interprétation.

Pandas est cependant un framework très très très riche et en faire le tour ici serait un vrai challenge (comme les autres frameworks au passage) cependant on va quand même essayer de faire ressortir les concepts principaux pour en déduire les utilisations les plus courantes.

Le concept principal de Pandas est, comme dans les langages dédiées aux sciences de données (comme R nous y reviendrons), le DataFrame.

Lorsque nous utilisions Numpy, nous représentions les données sous la forme de grande matrice ou les colonnes étaient des propriétés et les lignes des échantillons. Pourtant dans Numpy, tout cela était implicite et il fallait jongler avec des opérateurs pour extraire des données spécifiques.

Avec Pandas, tout cela est simplifier de façon a ce que les données soient nommées et traitable de la même manière que si elles étaient dans une SGBDR avec du SQL.

Commençons par le début: le chargement de données. Pandas est un facilitateur pour traiter la donnée, et cela commence par son chargement. Avec pas grand chose, il est aisé de charger un fichier au format csv afin de le transformer en mémoire en DataFrame.


1
2
import pandas as pd
learnSet=pd.read_csv('learnSet.csv',sep='\t')

Une fois que l'on dispose de cet objet initial, nous allons pouvoir l’ausculter. Mais alors quid de mes données et travaux fait avec Numpy?

Non les DataFrame sont des purs objets de la POO et ils fournissent un constructeur valué prenant en paramètre les matrices et les vecteurs Numpy. Il fourni alors un ensemble de fonctions entièrement dédiées à la manipulation des données et leur affichage.


Pour exemple, reprenons l'exemple de nos ananas et pastèques que nous utilisions dans l'article [4].
On va étiqueter nos données avec des 1 et des 0 pour les discriminer en ajoutant une colonne dédiée. En ensuite, on va construire quelques schéma en s'appuyant sur Seaborn [9]


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
import pandas as pd
import seaborn as sns
sns.set()
ones=np.mat(np.ones(len(ananas)))
zeros=np.mat(np.zeros(len(ananas)))
print(ananas.shape)
print(ones.T.shape)
print(np.concatenate((ananas,ones.T),axis=1))

pdAnanas=pd.DataFrame(np.concatenate((ananas,ones.T),axis=1))
#print(pdAnanas)
pdPasteques=pd.DataFrame(np.concatenate((pasteques,zeros.T),axis=1))
#print(pdPasteques)
datas=pdAnanas.append(pdPasteques)
datas.columns=["rugausité","couleur","forme","poid",'fruit']
#print(datas.head)
print(datas.size)

sns.pairplot(datas,vars=["rugausité","couleur","forme","poid"], hue='fruit', size=3,diag_kind='kde',palette="husl");


Nous donnant un schéma similaire a ceux obtenus a l’époque mais en plus rapide.


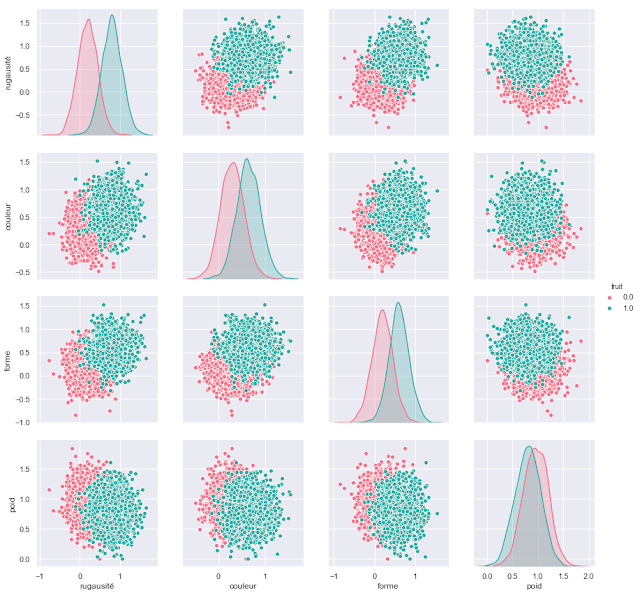
Je pense qu'il y a pas photo! En plus de cela, la structure de DataFrame est tel qu'il est plus simple de manipuler les données. Ainsi il est toujours possible par exemple de faire du slicing sur les données pour itérer ou extraire des sous-ensembles.

Mais ce n'est pas tout. On a vu que les colonnes sont nommés tout comme les lignes (en plus d'etre indexé) et cela permet de faire des pseudo requete. Ainsi en réalisant un appel comme on le ferait sur un dictionnaire, le DataFrame nous retournera un object Series qui contiendra la colonne ciblée:


1
2
3
4
5
6
datas["rugausité"] # sous le format tableau/dictionnaire
datas.rugausité # sous le format données membres
datas["rugausité"].values # sous le format Numpy

array([0.51557009, 0.83561812, 0.43919826, ..., 0.10898916, 0.18374726,
       0.2       ])

Ensuite bien sur il est possible d’itérer sur les lignes grâce a la méthode iterrows qui va nous renvoyer les différents tuples sur les données. Mais ce qui est le plus intéressant est, comme on l'a évoqué avec la comparaison avec SQL, la possibilité de construire des filtres sur les données.

Ainsi, il va être possible de, par exemple, extraire des données relevant de certains seuils. Par exemple essayons de conserver les données de forme sont inférieur a 1.


1
2
datas=datas[datas.forme<0.5]
sns.pairplot(datas,vars=["rugausité","couleur","forme","poid"], hue='fruit', size=3,diag_kind='kde',palette="husl");

Si on représente le résultat, on obtient le schéma suivant:



En utilisant ~ on pourra inverse le filtre ou utiliser drop_duplicates afin de supprimer les doublons dans un nouveau DataFrame.

Ainsi, on voit que Pandas, avec les DataFrame et les Series nous donne des outils de construction simple et efficace. De la même façon que Numpy avec les listes et les tableaux, Pandas va pousser plus loin de concept de dictionnaire (puisque nous allons retrouver des données indexé et des colonnes nommées, les Series).

On a vu aussi qu'il était possible de réaliser des projections ou filtrage, mais il est aussi possible de réaliser des pseudo union de Series en utilisant concat (le pendant de concatenate dans Numpy) ou mime utiliser merge pour joindre des DataFrame dont des Series seraient commune (équivalent a la jointure SQL) [10].

Conclusion

On pourrait aller beaucoup plus loin avec encore d'autres framework (nous nous intéresserons aussi au langage R qui reprend aussi le concept de DataFrame) mais ce n'est pas le but ici, puisque rappelons le, le but est de permettre d'avoir une première approche dans la manipulation des données dans le cadre du machine learning.

Désormais, on connait un peu quelques outils, nous allons pouvoir nous intéresser au framework de machine learning eux même comme Scikit-Learn.... bientot.

Références

[1] https://un-est-tout-et-tout-est-un.blogspot.com/2018/09/ia-equation-normale.html
[2] https://un-est-tout-et-tout-est-un.blogspot.com/2018/09/started-ia-neuromimetique-la-regression.html
[3] https://un-est-tout-et-tout-est-un.blogspot.com/2018/07/ai-approche-neuromimetique.html
[4] https://un-est-tout-et-tout-est-un.blogspot.com/2018/07/ai-approche-neuromimetique-la.html
[5] http://www.numpy.org/
[6] https://pandas.pydata.org/
[7] http://scikit-learn.org/stable/
[8] https://un-est-tout-et-tout-est-un.blogspot.com/2018/03/notions-de-mathematiques-elementaires.html
[9] https://seaborn.pydata.org/generated/seaborn.pairplot.html
[10] https://openclassrooms.com/fr/courses/4452741-decouvrez-les-librairies-python-pour-la-data-science/4740943-decouvrez-les-dataframes-et-la-librairie-pandas
Publié par à
Libellés : , , , , , , , , , , , , , , ,

Aucun commentaire:

Enregistrer un commentaire

Inscription à : Publier les commentaires (Atom)