IA : Neuromimétique, la régression linéaire

Nous revoilà sur un sujet un peu plus sympa pour ce début septembre, la régression linéaire.

Cet article aurait du être publié en août mais le temps a manqué, et j'ai voulu profiter du précédent article sur les Streams [1] pour essayer une approche un peu différente de ce tour d'horizon de ce que l'on peut faire avec un neurone!

Du coup aujourd'hui, il s'agit de présenter la régression linéaire en s'appuyant sur les Streams Java. Comme nous l'avions vu dans les articles précédents sur l'IA [2], nous allons créer un jeu de données d'apprentissage et un jeu de donnée de test sur deux cas d'utilisations (en fait 3 nous verrons pourquoi):

l'un sur l'identification de paramètres : nous allons donc demander a notre neurone de nous donner les paramètres (a,b) d'une droite tel que y=a.x+b
l'un sur la construction d'un modèle prédictif partant d'une droite bruité artificiellement (nous traiterons ici de plusieurs cas différents afin de considérer les situations qui marchent bien de celles, moins pertinentes)

Pour cela, nous n’utiliserons qu'un seul modèle de fonction d’activation : le linéaire [3]. Nous pourrions utiliser le sigmoïde mais ça risque de faire vraiment long... peut être que dans un autre article nous nous intéresserons a cette dernière.

Enfin concernant le mode d'apprentissage, nous utiliserons un apprentissage supervisé. Nous n'avions pas beaucoup parlé de ce point dans nos précédents articles sur la classification [2] [4], ou nous avions élaboré un modèle basé sur une correction simple du vecteur des paramétrés portés par les dendrites du neurone. Ici ça sera l'occasion de découvrir la descente de gradient [5] et par la même occasion quelques fonctions de coût nous permettant d’évaluer l'efficacité de notre modèle.

Pour bien comprendre cet article, je vais d'abord en donner les lignes directrices:

Tout d'abord, comme nous n'utilisons pas encore de frameworks spécifiques pour le machine learning (comme scikit-learn [6]) ou de framework de réseau de neurone comme Tensor-Flow [7] ou Keras [8]), il nous faut d'abord construire un neurone, lui donner une implémentation pour la fonction d'activation, et lui donner une fonction d'apprentissage.
Ensuite, nous tacherons de monitorer le neurone lors de son fonctionnement afin de nous permettre d'observer comment vont évoluer ses paramètres lors de l'apprentissage, et comment va évoluer son efficacité en fonction de ses paramètres.
Enfin, nous ferons une petite séance de visualisation de données sous python afin d'avoir des schémas explicatifs des données monitorées.

Voila, ça va être dense!

Le neurone

Nous en avions déjà fait un en python pour la classification. Ici on va aller a l'essentiel:

Un tableau de paramètre représentant les poids des dendrites (biais inclus).
Une fonction linearInfer permettant le calcul de la sortie du neurone (produit matricielle du vecteur d'entrée avec le vecteur des poids) inféré sur la fonction d'activation linéaire).
Une fonction d'apprentissage learnStep permettant la correction des poids selon des données étiquetés fourni par la classe Data
Quelques méthodes utilitaires comme la méthode reset permettant d'initialiser les données des poids de façon aléatoire.

public class Neurone {

    public Double[] dendrites;

    public Neurone(int inSize)
    {
        this.reset(inSize);
        System.out.println(this);
    }

    public void setParameter(Double v,Double b)
    {
        this.dendrites[0]=v;
        this.dendrites[1]=b;
    }

    public void reset(int inSize)
    {
        this.dendrites= Stream.generate(() -> Math.random()/1000).limit(inSize+1).toArray(Double[]::new);
    }

    public Double linearInfer(Double[] stepInputs)
    {
        ...      
    }

    public void learnStep(Set<Data> datasSet)
    {
        ...
    }

}

public class Data {

    public Double[] input;
    public Double output;


    public Data(Double[] input,Double output)
    {
        this.input=input;
        this.output=output;

    }
}

Nous voila donc une ébauche de neurone et une structure de données pour gérer les données d'apprentissage.

Inference

Maintenant, intéressons nous a l’implémentation de la méthode linearInfer. Il s'agit ici de réaliser le produit matriciel du vecteur d'entrée avec les poids du neurone afin d'obtenir une sortie estimée (y chapeau):

$\widehat{y} = W^T.X + b$

(A noter que le paramètre b est selon les modèles négatif ou positif, donc selon le cas le modèle mathématique du neurone peut se s’écrire avec un + ou -)

En java on aura alors:

public Double linearInfer(Double[] stepInputs)
{
    Stream.Builder<Double> sum=Stream.<Double>builder();
    for(int i=0;i<dendrites.length;i++)
    {
        if(i<stepInputs.length)
            sum.add(dendrites[i]*stepInputs[i]);
        else
            sum.add(dendrites[i]);
    }
    return sum.build().reduce((x,y)-> x+y).get();;
}

L'apprentissage

Pour implémenter la fonction d’apprentissage, il va nous falloir entrée dans quelques considérations mathématiques. En effet, l'apprentissage implique qu'il y ait amélioration et pour qu'il y ait amélioration, il faut être capable de mesurer sa performance.

Ainsi nous avions vu dans l'article [9], une fonction classique de mesure de la performance: la Mean Quare Error (ou MSE) ou aussi la Root Mean Square Error (ou RMSE). La seconde étant la racine carré de la premier, elle sont au facteur prêt équivalente, la seconde est néanmoins peut être plus coûteuse en terme de calcul:

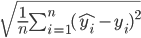
L'idée de l’apprentissage est donc de trouver les paramètres de notre neurone dont les réponses suite a l’inférence permettront de minimiser cette fonction. Pour cela, Nous utiliserons la descente de gradient. Quoi ??? c'est quoi ça???? (Note : la minimisation de la fonction de coût peut être résolu analytiquement par la formule de l’équation normale, nous ne la traiterons pas ici mais dans un article prochain)

Explication du pourquoi de la descente de gradient: Dans le principe nous venons de voir que nous souhaitions minimiser la fonction de coût (la MSE). Pour se faire en mathématique, sur les fonctions ça se traduit par la recherche des valeurs annulant la dérivée. Ainsi si l'on dérive notre fonction de coût, la tache que nous aurons sera de trouver les paramétrés du neurone pour lesquels cette dérivée est nulle et Bingo! ces paramètres seront théoriquement les meilleurs.

Sauf que... lorsque le nombre de paramètres est élevé, la résolution peut être très difficile, voir impossible ou alors trop coûteuse en terme de temps de calcul informatique.

Ainsi une autre façon de faire est de revenir a la définition même de la dérivée, c'est a dire le coefficient directeur de la droite tangente a la fonction au point considéré selon les différents paramètres de notre modèle.

Ainsi en partant du principe que la fonction de coût est continue-ment dérivable, la descente de gradient propose de descendre la pente de la fonction en suivant l'orientation prise par la dérivée calculée a chacun des pas à chaque ajustement des paramètres du modèle [5].

Donc en résumé, la descente de gradient propose de calculer la pente de la fonction de coût localement en fonction du paramétrage du modèle et calculer une pente, contrairement à une dérivé c'est carrément plus simple.

Dans notre cas, nous n'utiliserons pas la MSE mais la MAE (Mean Absolute Error). Il s'agit d'une autre façon de calculer l'erreur moyenne de notre modèle tout en nous évitant, des passages a la puissance ou des racines:

$MAE(W)=\frac{1}{n} \sum_{i=1}^n | \hat{y^i}-y^i | = \frac{1}{n} \sum_{i=1}^n | W^T.X^i-y^i |$

Ainsi afin de corriger nos paramètres, a chaque itération, nous allons retrancher aux paramètres, la valeur obtenu par le coefficient de la pente de la MAE calculé en ce point, soit:

$W_{k+1}=W_{k} - \eta . \frac{\partial MAE(W_k)}{\partial W_k}$

avec un coefficient (que l'on appelle soit coeficient d'amortissement, soit taux d'apprentissage, il correspond au pas de l’itération et peut accélérer la convergence, ou le contraire....)

Dans le détail, le gradient de la MAE nous donne alors ceci:

$\nabla MAE(W)= \frac{\partial MAE(W_k)}{\partial W_k}=\frac{1}{n} \sum_{i=0}^n (x_k^i).( \hat{y^i}-y^i)$

On a vu beaucoup de chose théorique la du coup, maintenant voyons comment nous pouvons implémenter cela en Java.

Implémentation de l'apprentissage

Tout d'abord il nous faut une implémentation de la MAE, cela nous permettra lors des phases d'apprentissage d’apprécier l’évolution de la performance de notre modèle.

public Double MAE(Set<Data> datasSet)
{
    Double eccartAbsolue=datasSet.stream()
            .map(x ->x.input[0]*Math.abs( this.linearInfer(x.input)-(x.output)))
            .reduce((x,y) -> x+y).get();
    System.out.println("Calcul MAE : "+eccartAbsolue/datasSet.size());
    return eccartAbsolue/datasSet.size();
}

Ensuite il nous faut les fonctions permettant de calculer les pentes de la MAE selon les deux paramètres que nous avons, la pente et le biais.

public Double MAEpente(Set<Data> datasSet)
{
    Double eccartAbsolue=datasSet.stream()
            .map(x ->x.input[0]*( this.linearInfer(x.input)-(x.output)))
            .reduce((x,y) -> x+y).get();
    System.out.println("Calcul MAEpentre : "+eccartAbsolue/datasSet.size());
    return eccartAbsolue/datasSet.size();
}

public Double MAEbiais(Set<Data> datasSet)
{
    Double eccartAbsolue=datasSet.stream()
            .map(x ->(  this.linearInfer(x.input)-(x.output)))
            .reduce((x,y) -> x+y).get();
    System.out.println("Calcul MAEbiais : "+eccartAbsolue/datasSet.size());
    return eccartAbsolue/datasSet.size();
}

Du coup nous avons la toutes les briques pour nous permettre d’implémenter une fonction d'apprentissage basé sur la descente de gradient.

private Double ammortissement=0.0003;

public void learnStep(Set<Data> datasSet)
{
    Double MAEpente=this.MAEpente(datasSet);
    Double MAEbiais=this.MAEbiais(datasSet);
    maeDescent.append(dendrites[0]).append("\t")
            .append(dendrites[1]).append("\t").append(MAEpente).append("\t").append(MAEbiais).append("\n");
    dendrites[0] = dendrites[0] - ammortissement*MAEpente;
    dendrites[1] = dendrites[1] - 1000*ammortissement*MAEbiais;
    ammortissement=ammortissement/1.01;
}

Dans cette fonction, on calcule les deux MAE pour les deux directions, puis on ajuste les poids en fonction. On utilise un coefficient d'amortissement afin d'avoir un incrément cohérent dans la recherche du minima et on réajuste ce coefficient de façon a ne pas passer au dessus et osciller.

On notera la concaténation (un peu brute) des données dans une structure afin de permettre la visualisation des données (au prochain chapitre). Dans la continuité de l'idée, nous allons a cela ajouter quelques fonctions permettant de consolider les données produites afin de pouvoir les données aux outils de visualisation matplotlib de python.

Dans un premier temps, une fonction pour sérialiser dans un fichier le jeux de donnée d'apprentissage

private static void  toData2File(String path,Set<Data> datas)
{
    File f=Paths.get(path).toFile();
    if(f.exists())
        f.delete();
    try(PrintWriter writer=new PrintWriter(Files.newBufferedWriter(Paths.get(path), StandardCharsets.UTF_8)))
    {
        f.createNewFile();
        writer.println("output\tinput");
        datas.stream().forEach(x-> writer.println(x.toPandas()));
    }
    catch (IOException ioe) {
        ioe.printStackTrace();
    }
}

Ensuite une fonction pour sauvegarder de la meme maniere les données produites:

private static void saveResult(String path,StringBuilder b)
{
    File f= Paths.get(path).toFile();
    if(f.exists())
        f.delete();
    try(BufferedWriter writer=Files.newBufferedWriter(Paths.get(path), StandardCharsets.UTF_8))
    {
        f.createNewFile();
        writer.write(b.toString(),0,b.length());
    }
    catch (IOException ioe) {
        ioe.printStackTrace();
    }
}

Ensuite pour parfaire la visualisation des données, il y a un type de données qu'il peut être intéressant de présenter, celui des cartes de performance de la fonction de coût.

Carte de performance

Lorsque nous avions parler de la fonction de coût (la MSE ou la MAE), nous avons évoqué que le but était de minimiser cette fonction. Dans le cadre de modèles relativement simple (avec peu de paramètre ... comme ici avec un modèle linéaire), il est possible de construire des cartes représentatives de ce coût (ou performance) en fonction de plages de valeurs possibles des paramètres du modèle.

Ces cartes sont intéressantes car elles fournissent un moyen simple de visualiser les minima, les maxima, l'orientation des pentes, etc. Ainsi couplé a l’évolution des paramètres lors de l'entrainement, il est alors possible de voir comment se déplace notre apprentissage dans l'espace des paramètres du modèle.

A noter que ces cartes ne sont utilisables que dans les cas simples pour la compréhension du modèle car lorsque le jeu d'apprentissage est trop conséquent o/et que l'espace des paramètres à explorer est trop grand, la quantité de calcul a réaliser pour obtenir des informations intéressante peut être rapidement rédhibitoire.

Pour construire cette carte nous allons alors avant de réaliser l’apprentissage explorer l'espace des paramètres comme suit avec la fonction generateMAEMap.

public static void generateMaeMap(Neurone n,Set<Data>  dataSet)
{
    StringBuilder maeMap=new StringBuilder();
    maeMap.append("pente").append("\t");
    maeMap.append("bias").append("\t");
    maeMap.append("maePente").append("\t");
    maeMap.append("maebiais").append("\t");
    maeMap.append("mae").append("\n");
    for(int i=-50;i<50;i++)
    {
        for(int j=-50;j<50;j++)
        {
            n.setParameter(Double.valueOf(i),Double.valueOf(j));
            Double maePente=n.MAEpentre(dataSet);
            Double maebiais=n.MAEbiais(dataSet);
            Double mae=n.MAE(dataSet);
            maeMap.append(i).append("\t");
            maeMap.append(j).append("\t");
            maeMap.append(Math.abs(maePente)).append("\t");
            maeMap.append(Math.abs(maebiais)).append("\t");
            maeMap.append(Math.abs(mae)).append("\n");
        }
    }
    saveResult("out/maeMap.csv",maeMap);
}

Voila nous avons notre neurone, nous avons l’inférence, une mesure de performance et une méthode d'apprentissage basé sur la descente de gradient et quelques fonctions utiles a l'exploitation des données.

Il ne reste plus qu'a coordonner tout cela dans un processus main de production de jeu de données et d'apprentissage (dans l'exemple ci dessous, nous aurons deux types de jeux de données, le premier pour l'identification, cas le plus simple, le second pour de la vrai régression selon plusieurs situations)

MAIN

Neurone n=new Neurone(1);
Set<Data>  dataSet=getSimpleModel(-100.0,20.0, 30.0);
//Set<Data>  dataSet=getBruiteModel(-100.0,20.0, 30.0);
generateMaeMap(n,dataSet);
n.reset(1);
apprentissage(n,dataSet);

Avec pour fonction apprentissage l’implémentation suivante:

public static void apprentissage(Neurone n,Set<Data>  dataSet)
{
    System.out.println("Phase d'apprentissage");
    Double eccart=Double.MAX_VALUE;
    //n.setParameter(-40.0,-40.0); // ca c'est si on souhaite donner des valeur de depart specifique et non aleatoire
    int iteration=0;
    StringBuilder mae=new StringBuilder("pente\t").append("biais").append("\t").append("maeEvol").append("\n");
    while(eccart> 0.001 && iteration <100000)
    {
        System.out.println("Iteration:"+iteration++);
        n.learnStep(dataSet);
        eccart=Math.abs(n.MAE(dataSet));
        mae.append(n.dendrites[0]).append("\t").append(n.dendrites[1]).append("\t").append(eccart).append("\n");
    }

    saveResult("out/maeDerEvol.csv",n.getDescent());
    saveResult("out/maeEvol.csv",mae);
}

Voila nous avons maintenant toutes les clefs pour démarrer nos exemples.

Identification

Voici dans le premier exemple de l'utilisation de notre neurone. Il s'agit du cas le plus simple car Nous allons traité de l'identification de paramètres via la régression.

Dans un premier temps il nous faut des données. Bien sur nous allons les produire nous même en proposant la fonction getSimpleModel suivante:

public static Set<Data> getSimpleModel(Double initValue,Double pente,Double ori)
{
    Set<Data> dataSet=Stream.iterate(initValue,x -> x+1).limit(200)
            .map(x->new Data(Stream.<Double>builder().add(x).build().toArray(Double[]::new),pente*x+ori))
            .collect(Collectors.toSet());

    toData2File("out/learnSet.csv",dataSet);
    return dataSet;
}

Ensuite il reste a appliquer le code précédemment tagger MAIN. Ce code nous produit alors 4 fichiers que nous allons traiter avec python dans un notebook Jupyter:

learnSet.csv
maeDerEvol.csv
maeEvol.csv
maeMap.csv

Nous allons profiter du fait que l'exemple est simple pour aussi nous intéresser sur comment visualiser nos données. Cela nous évitera de nous perdre dans les détails techniques lors de l'exploration des données pour la régression linéaire qui viendra ensuite.

Preparatif

Tout d'abord quelques imports

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import cm
import math

Ensuite on va se définir deux fonctions utilitaire qui nous faciliterons la vie pour représenter nos données

def matAbs(A,B):
    Z=[]
    for i in range(0,len(A)):
        if A[i]>B[i] :
            Z.append(A[i])
        else:
            Z.append(B[i])
    return np.array(Z)

def matlog(D):
    DAT=[]
    for i in D:
        if i!= 0:
            DAT.append(math.log(abs(i)))
        else :
            DAT.append(i)
    return np.array(DAT)

La première est une fonction permettant simplement fusionner deux listes de données mapper sur des coordonnées similaires mais d'en garder le max des deux. Cette fonction sera utile pour conserver le max de deux cartes que l'on voudra superposer.

La seconde est une fonction prenant le log d'une liste de donnée afin d'en réduire la représentation a une croissance logarithmique ce qui est souvent très pratique pour des données de valeur absolue élevée.

Chargement des données

Maintenant chargeons les données et donnons leur une représentation des plus basiques, leur trois premières valeurs. Pour cela on utilise Pandas.

learnSet=pd.read_csv('dataRegressionFromJava/learnSet.csv',sep='\t')
maeDerEvol=pd.read_csv('dataRegressionFromJava/maeDerEvol.csv',sep='\t')
maeEvol=pd.read_csv('dataRegressionFromJava/maeEvol.csv',sep='\t')
maeMap=pd.read_csv('dataRegressionFromJava/maeMap.csv',sep='\t')
print(learnSet[:3])
print(maeDerEvol[:3])
print(maeEvol[:3])
print(maeMap[:3])

Cela nous affiche:

   output  input
0  1350.0   66.0
1   -70.0   -5.0
2  -370.0  -20.0
      pente     biais     MAEpentre   maeBiais
0  0.000396  0.000287 -66653.681412 -19.999911
1  3.999616  1.200281 -53322.878590 -20.799527
2  7.198989  2.448253 -42658.393629 -21.151242
      pente     biais     maeEvol
0  3.999616  1.200281  639.838760
1  7.198989  2.448253  737.350307
2  9.758493  3.717328  801.781860
   pente  bias  maePente  maebiais     mae
0    -50   -50  233305.0      45.0  499.90
1    -50   -49  233305.5      44.0  449.91
2    -50   -48  233306.0      43.0  399.92

Ok, donc nous avons

un ensemble de jeux de données.
l’évolution au fil de l'apprentissage des differentes dérivées de la MAE selon leur paramètre associée
l’évolution de la MAE en fonction des paramètres du modèle
les valeurs de la MAE et de ses dérivées dans l'espace des valeurs [-50;50] des paramètres du modèle

Le jeu de données

Commençons par visualiser le jeu de donnée (le code presenté ici sera le meme pour les autres exemples)

fig = plt.figure(1,figsize=(8,8))
X=  np.arange( 0, len(learnSet) )
LEARNSET=np.array(learnSet)

plt.plot(LEARNSET.T[1],LEARNSET.T[0],"b.")

Produisant le schéma ou l'on constate une droite d’équation y=20*x+30 (en fait les paramètre donnés dans le code java a la fonction getSimpleModel)

Bon du coup la question c'est : est ce que notre model a convergé?

Pour savoir cela, nous allons regarder si les paramètres du modèle ont trouvé une limite et si la MAE tend vers 0 (nous pourrions nous attarder sur la notion de limite mathématique mais le schéma sera suffisamment explicite).

fig = plt.figure(1,figsize=(8,8))
X=  np.arange( 0, len(maeEvol) )
MAEEVOL=np.array(maeEvol)
plt.plot(X,MAEEVOL.T[0],"r-")
plt.plot(X,MAEEVOL.T[1],"b-")
plt.plot(X,matlog(MAEEVOL.T[2]),"g-")

Alors on constate bien que nous avons convergé. La pente du modèle linéaire est identifié a 20 et celle du biais a 30. Attention la courbe verte peut être trompeuse a la lecture. Il s'agit de la MAE représenté selon une échelle log donc la elle fini négative, signifiant que la MAE finie inférieur a 1.

OK sur un modèle simple ca marche plutôt bien mais pourquoi ça marche?

Pour comprendre cela, je vous propose de nous intéresser a la carte de performance de la fonction de cout, la MAE. Visualisons la selon differents angles:

MAEMAP= np.array(maeMap)

X = MAEMAP.T[0].reshape(100,100)
Y = MAEMAP.T[1].reshape(100,100)


#??? en log ou pas en log    
Z = MAEMAP.T[4].reshape(100,100)

fig = plt.figure(1,figsize=(15,15))
ax = plt.subplot(221, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
ax.view_init(40, 40)
ax = plt.subplot(222, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
ax.view_init(40, 75)
ax = plt.subplot(223, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
ax.view_init(40, 110)
ax = plt.subplot(224, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
ax.view_init(40, 150)

OK la MAE a une forme bizarre que l'on ne comprend pas vraiment. On dirait deux surface en intersection avec comme une sorte de fissure sur l'axe de pente valant 20. L’interprétation peut sembler compliqué mais en fait, ça ne l'est pas tant que ça

En fait si on essaye de comprendre pourquoi cette faille, c'est simplement que toute droite ayant une pente de 20 peut accepter n'importe quelle valeur a l'origine sans compromettre fondamentalement le modèle. C'est pour cela que la brisure est brutale. En fait on comprend par la que la sensibilité du modèle est surtout conditionné par la pente et non le biais.

De son coté, la grande vallée que l'on peut observé est du au fait que certaines combinaisons (pente,biais) sont des modèles acceptable selon le point de vu du jeux de données.

Attention aussi a l'effet d'optique de croire que cette vallée est plane, en fait elle a une pente faible. Pour s'en convaincre, il suffit d'apposée les differentes itérations d'apprentissage sur le schéma et l'on se rend bien compte que l'on ne "remonte" pas cette vallée.

MAEMAP= np.array(maeMap)

X = MAEMAP.T[0].reshape(100,100)
Y = MAEMAP.T[1].reshape(100,100)
Z = abs(MAEMAP.T[4].reshape(100,100))

fig = plt.figure(1,figsize=(15,15))
ax = plt.subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis, alpha=0.5)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10, alpha=0.5)

X = MAEEVOL.T[0]
Y = MAEEVOL.T[1]
Z = MAEEVOL.T[2]

ax.scatter(X,Y,Z,c="r")

ax.view_init(40, 60)

On voit bien ici que au fil des itérations d'apprentissage, on va converger vers l'intersection des deux vallées en (20,30)

Enfin si l'on s'amuse a construire la conjonction des dérivées de la MAE a l'aide de l'autre jeux de données, on se rend compte alors de manière encore plus marqué que celle ci forme une cuvette dont les parallèles aux lignes de niveaux convergent vers le minimal optimal de la MAE.

fig = plt.figure(1,figsize=(15,15))

ax = plt.subplot(111, projection='3d')
MAEMAP= np.array(maeMap)
X = MAEMAP.T[0].reshape(100,100)
Y = MAEMAP.T[1].reshape(100,100)
Z = abs(matAbs(MAEMAP.T[2]/5000,MAEMAP.T[3])).reshape(100,100)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
ax.view_init(55, 225)

X2 = MAEDEREVOL.T[0]
Y2 = MAEDEREVOL.T[1]
Z2 = MAEDEREVOL.T[2]
Z22 = MAEDEREVOL.T[3]


fig = plt.figure(1,figsize=(15,15))
ax = plt.subplot(111, projection='3d')
MAEMAP= np.array(maeMap)
X = MAEMAP.T[0].reshape(100,100)
Y = MAEMAP.T[1].reshape(100,100)
Z = abs(matAbs(MAEMAP.T[2]/5000,MAEMAP.T[3])).reshape(100,100)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis,alpha=0.5)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10,alpha=0.5)

ax.scatter(X2,Y2,Z2,c="r")
ax.scatter(X2,Y2,Z22,c="g")

ax.view_init(90, 225)

Voila une belle descente de gradient et les deux derniers schéma parlent d'eux même je pense. Ceci était pourtant le cas simple ou nos données sont celles d'une droite.

La régression linéaire

Explorons maintenant le cas ou l'on se base sur des données bruités selon différents contextes.

Pour cela il faut utilisé un autre modèle java de production des données:

    public static Set<Data> getBruiteModel(Double initValue,Double pente,Double ori)
    {
        Supplier<Double> bruit=() -> (Math.random()-0.5)*200;
        Set<Data> dataSet=Stream.iterate(initValue,x -> x+1).limit(200)
                .map(x->new Data(Stream.<Double>builder().add(x).build().toArray(Double[]::new),(pente*x+ori)+bruit.get()))
                .collect(Collectors.toSet());

        toData2File("out/learnSet.csv",dataSet);
        return dataSet;
    }

De la même manière que précédemment, les fichiers de données seront les mêmes. Et les codes python également, par contre attention, de façon a ne pas partir vainqueur, je ne donnerai pas les paramètres ayant permis la création du jeux de données, comme, pas de biais dans l'analyse.

Cas d’étude 1

Comme premier jeux de données, considérons un cas bruité mais simple (avec une dispersion relativement faible et un jeux de données suffisamment conséquent)

Avec un jeu de données comme celui la, notre modèle ne devrait pas trop avoir de mal a converger.

Effectivement, les paramètres du modèles convergent assez efficacement vers les valeurs de 35 et 20 réciproquement pour le biais et la pente. Par contre on constate que la minimisation de la MAE tend vers une valeur minimale, un peu inférieur 5. Ainsi on se rend compte ici d'une première contrainte qu'il faut prendre en compte lors de l'apprentissage. La dispersion des valeurs aura un impact sur la valeur du minimum atteignable de la fonction de coût (effectivement un modèle associée a une MAE nulle pourrait être considéré comme parfait, mais c'est impossible).

Dans notre algorithme d'apprentissage, il est donc nécessaire de savoir définir un seuil de la MAE, suffisamment satisfaisant mais atteignable pour considérer que notre modèle est adapté.

Cas d’étude 2

Dans ce cas d’étude, nous allons nous mettre dans une situation ou l'on est pauvre en données comme sur le schéma suivant:

Avec si peu de données, même si nous humain, nous sommes capable de deviner une droite directrice, on peut se demander s'il est possible d'extraite un modèle pertinent. Regardons donc le comportement et l’évolution des paramètres du modèles lors de l'apprentissage.

Ah! Mais ca va en fait! La MAE tend vers 0! Ca signifie que l'on a convergé!!

Oui mais... Si l'on regarde plus attentivement, on se rend compte que l'apprentissage semble s’être arrêter trop tôt. En effet les courbes de l’évolution de paramètres ne semble pas avoir une asymptote horizontale (ce qui a priori devrait arriver si le modèle était aller assez loin).

Bon vous allez dire : on va pas chipoter, on a une MAE proche de zero donc, normalement nos paramètres sont bons! (autour de 12 et 20 semble t il)

Ok c'est vrai, ça devrait être satisfaisant mais... intéressons nous a la carte de performance pour nous faire une idée:

Euh... qu'est ce qui s'est passé? Pourquoi les vallées se sont élargies? En fait, c'est plutôt simple, avec peu de données, l'espace des modèles valables pour satisfaire le jeu de donnée est d'autant plus grand que les données sont pauvres. Ainsi, forcement la zone permettant de minimiser la MAE est d’autant plus grande et plane.

Ce que l'on doit en retenir? C'est que finalement le modèle obtenu n'aura pas forcement la robustesse nécessaire pour résister a de nouvelles données et être fiable (mais en fait on aurait pu facilement s'en douter) même en poursuivant l'apprentissage plus longtemps.

Cas d’étude 3 (bonus stage)

Bien, pour ce dernier exemple, nous allons revenir a un jeu de donnée linéaire (comme dans le cas du problème de l'identification).

Pourquoi? Et bien nous allons un peu trifouiller le paramètre d’amortissement de l'algorithme de descente de gradient pour observer un phénomène assez intrigant. Observons cela directement sur la carte de performance sur laquelle on va faire apparaître comme précédemment l’évolution de la MAE au fil de l'apprentissage.

Euh on dirait qu'il y a deux chemins de descente du gradient! Comment c'est possible ? J'avais dit que ça serait bizarre! Pour comprendre ce phénomène, il suffit en réalité de regarder l’évolution des paramètres du modèle:

Ça y est vous avez compris? Et oui c'est ça, selon le paramétrage, différents modes de fonctionnement peuvent apparaître dans lors de la phase d'apprentissage et la, notre apprentissage suit un mode convergent mais oscillatoire en sautant d'un coté de l'autre de la vallée.

En fait, jusqu'ici, nous avons considéré que l'algorithme était forcement convergent, sauf que ce n'est pas forcement le cas, bien au contraire. Alors bien sur il n'y avait pas beaucoup d’intérêt a s'attarder sur les apprentissages divergents et il est logique d’étudier ceux fournissant des résultats (plus ou moins bon comme nous l'avons vu). Cependant, l'ajustement du coefficient d’amortissement n'est pas forcement simple et demande quelques essais avant de donner des résultats "au moins convergent".

Ainsi, C'est lors de ces essais, ou l'on essaye d'ajuster l'algorithme de descente de gradient, que l'on peut tomber sur ce genre de système oscillant ou le paramétrage va converger mais sauter d'un coté a l'autre des pentes de la vallée.

Conclusion

Et bien voila, nous voila au bout de cet article mais aussi au bout de se tour d'horizon de ce que l'on peut faire avec un neurone. Nous avions vu de la classification et ici de la régression. Nous en avons profité pour voir des algorithmes d'optimisation, des fonctions de coûts (MAE, MSE) et aussi des concepts clefs comme les matrices de confusion, etc....

L'idée était bien sur de donner des explications au plus prêt de l’implémentation de façon a bien comprendre les tenant et le fonctionnement intime de cette partie de l'IA.

Dans les prochains articles, pour gagner du temps et parce que ici nous avons déjà vu un bon paquet de concepts de base, nous nous appuierons plus sur des frameworks existant [6-7-8] de façon a d'une part soit allez plus a l'essentielle (comme prochainement avec l’équation normale) soit monter en puissance sur des exemples plus intéressant et plus "utiles" (nous verrons cela...)

Note: Cet article a été long et n'est probablement pas sans erreurs, fautes ou méprises, n’hésitez pas a me les remonter le cas échéant.

Références

[1] https://un-est-tout-et-tout-est-un.blogspot.com/2018/08/les-streams-avec-java-8.html
[2] https://un-est-tout-et-tout-est-un.blogspot.com/2018/07/ai-approche-neuromimetique-la.html
[3] https://un-est-tout-et-tout-est-un.blogspot.com/2018/07/ia-approche-neuromimetique-le-neurone.html
[4] https://un-est-tout-et-tout-est-un.blogspot.com/2018/07/ai-approche-neuromimetique.html
[5] http://www.math-info.univ-paris5.fr/~bouzy/Doc/AA1/DescenteGradient.pdf
[6] http://scikit-learn.org/stable/
[7] https://www.tensorflow.org/
[8] https://keras.io/
[9] https://un-est-tout-et-tout-est-un.blogspot.com/2018/03/notions-de-mathematiques-elementaires.html

Un est tout et tout est un

Thématiques principales

dimanche 9 septembre 2018